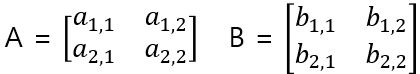
이미지 출처: PPT 수식 캡쳐
선형대수학에서 슈트라센 알고리즘은 독일의 수학자 폴커 슈트라센(Volker Strassen)이 1969년에 개발한 행렬 곱셈 알고리즘이다. 정의에 따라 n×n 크기의 두 행렬을 곱하면 O(n3)의 시간이 소요되지만 이 알고리즘은 대략 O(n2.807)의 시간이 소요된다.
일반적으로 행렬의 곱셈은 A(ixj) , B(kxl) 일 때 AxB 행렬의 크기는 AxB(ixl)이 된다. 이 글에서는 스트라센 알고리즘을 위해 정방행렬을 사용할 것이다.
우리가 일반적으로 사용하는 행렬의 곱셉이다.
nxn 크기의 정사각 행렬을 곱하면 총 n2번의 곱셈과 (n-1)n2번의 덧셈을 한다. O(n3)의 시간이 소요된다.
이미지 출처: PPT 수식 캡쳐
C1,1 =
(A1,1 x B1,1 + A1,2 x B2,1)
C1,2 =
(A1,1 x B1,2 + A1,2 x B1,2)
C2,1 =
(A2,1 x B1,1 + A2,2 x B2,1)
C2,2 =
(A2,1 x B1,2 + A2,2 x B2,2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class Main {
public void name() {
/* 두 행렬 a, b */
int[][] a = { { 1, 2 }, { 3, 4 } };
int[][] b = { { 1, 2, }, { 3, 4 } };
/* 결과값 행렬 c */
int size = 2;
int[][] c = new int[size][size];
/* 두 행렬의 곱셈 */
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
for (int h = 0; h < size; h++) {
c[i][j] += a[i][h] * b[h][j];
}
}
}
/* 값이 나온 각각의 값을 출력 */
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
System.out.println(c[i][j] + "");
}
}
}
/* Main */
public static void main(String[] args) {
/* 실행 */
Main m = new Main();
m.name();
}
}
스트라센 알고리즘에서 행렬의 곱셉을 더하기 연산으로 분할하여
각 원소를 구할 수 있는 M행렬로 표현한다.
M행렬은 일곱번의 곱셈과 10번의 덧셈으로 연산으로 나타낼 수 있다.
M1 = (A1,1 + A2,2)(B1,1 + B2,2)
M2 = (A2,1 + A2,2)B1,1
M3 = A1,1(B1,2 - B2,2)
M4 = A2,2 (B2,1 - B1,1)
M5 = (A1,1 + A1,2)B2,2
M6 = (A2,1 - A1,1)(B1,1 + B1,2)
M7 = (A1,2 - A2,2)(B2,1 + B2,2)
결과값인 C행렬은 위의 M행렬의 더하기 연산으로 이루어진다.
C1,1 = M1 + M4 - M5 + M7
C1,2 = M3 + M5
C2,1 = M2 + M4
C2,2 = M1 - M2 + M3 + M6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
public class Strassenpractice {
public void na() {
System.out.println("시작");
int[][] a = { { 1, 2 }, { 3, 4 } };
int[][] b = { { 1, 2 }, { 3, 4 } };
/* a행렬 값 나누기 */
int a11 = a[0][0];
int a12 = a[0][1];
int a21 = a[1][0];
int a22 = a[1][1];
/* 값이 잘 나오는지 확인 */
System.out.println(a11);
/* b행렬 값 나누기 */
int b11 = b[0][0];
int b12 = b[0][1];
int b21 = b[1][0];
int b22 = b[1][1];
/* 값이 잘 나오는지 확인 */
System.out.println(b11);
/* m을 구하기 위한 연산 */
int m1 = (a11 + a22) * (b11 + b22);
int m2 = (a21 + a22) * b11;
int m3 = (a11) * (b12 - b22);
int m4 = a22 * (b21 - b11);
int m5 = (a11 + a12) * b22;
int m6 = (a21 - a11) * (b11 + b12);
int m7 = (a12 - a22) * (b21 + b22);
/* 값이 잘 나오는지 확인 */
System.out.println(m1);
int[][] c = new int[2][2];
c[0][0] = m1 + m4 - m5 + m7;
c[0][1] = m3 + m5;
c[1][0] = m2 + m4;
c[1][1] = m1 - m2 + m3 + m6;
/* c행렬 합치기 */
for (int i = 0; i < c.length; i++) {
for (int j = 0; j < c.length; j++) {
System.out.println(c[i][j]);
}
}
}
}
/* Main */
public static void main(String[] args) {
/* 실행 */
Strassenpractice sp = new Strassenpractice();
sp.na();
}
Strassen Algorithm은 정사각 행렬만을 처리한다.
만약 행렬이 정사각 행렬이 아닌 경우,
정사각 행렬로 변형시켜줘야 한다.
M행렬을 구하는 과정에서 행렬의 곱이 사용된다.
행렬의 곱을 스트라센 알고리즘이라고 생각하면 재귀적 호출을 통해
M행렬을 구할 수 있다.
행렬을 작은 단위로 분할하여 M행렬을 구하고 결과값 C행렬을 구할 수 있다.
일반 행렬곱[O(n3)]과 스트라센 알고리즘을 이용한 행렬 곱[O(n2.807)]의 시간복잡도는 크게 차이가 많이 나는 것 같지 않아
보여도 nxn 정사각 행렬에서 n의 값이 커질수록 큰 차이를 보인다.
스트라센 알고리즘을 코드로 구현해 보았다. 분할 정복 알고리즘에 알맞는 코드는 아니라는 생각이든다. 분할 정복 알고리즘은 값을 분할 하는것이 중요하다고 생각이 든다. 앞으로 조금 더 알고리즘 다운 코드를 짜기위해 노력해야 겠다.