- x[t]는 입력배열이고 X[k]는 변환된 배열이다.
(k = 0,1,2,…N-1)
이미지: PPT캡쳐
- WN과 j의 값이다.
이미지: PPT캡쳐
FFT(고속 푸리에 변환 알고리즘) 알고리즘을 보기전에 DFT(이산 푸리에 변환)을 간단히 알아보자.
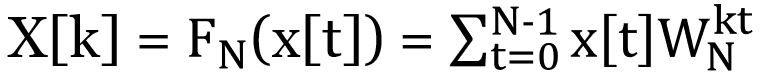 이미지: PPT캡쳐
이미지: PPT캡쳐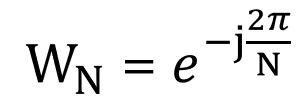
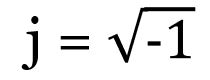 이미지: PPT캡쳐
이미지: PPT캡쳐DFT 식을 짝수항과 홀수항으로 풀어보면 아래와 같다.
X[k] = ∑N-1t=0 x[t]WknN(n=짝수) + ∑N-1t=0 x[t]WknN(n=홀수)
= ∑(N/2)-1m=0 x[2m]W2mkN + ∑(N/2)-1m=0 x[2m+1]W(2m+1)kN
= ∑(N/2)-1m=0 x[2m]W2mkN + W2mkN ∑(N/2)-1m=0 x[2m+1]W2mkN
위 식에서 W2N는 W2N = e-j2π/(N/2) = W1N/2 와 같다.
X[k]를 아래와 같이 정의할 수 있다. (0 <= k = N/2)
X[k] = ∑(N/2)-1m=0 x[2m]WmkN/2 + WkN ∑(N/2)-1m=0 x[2m+1]WmkN/2
두 항을 각각 A[k], B[k]로 생각하면 X[k] = A[k] + WkN B[k]로 나타낼 수 있다.
X[k+ N/2]를 아래와 같이 정의할 수 있다. (N/2 <= k = N) k가 N/2보다 클 경우 회전인자는
Wk+N/2N = e-j2π(k+N/2)/N = e-j2πk/N * e-j2πkN/2N = WkN * e-jπ 오일러 법칙에 의하여 WkN * e-jπ = WkN * (cosπ - jsinπ) = -WkN 이 된다.
따라서 N/2 <= k 일 경우에서 X[k]는 X[k] = A[k] - WkN B[k]로 나타낼 수 있다.
X[k] = A[k] + WkN B[k]와 X[k] = A[k] - WkN B[k]를 더하여 DFT를 진행해 주면 변환된 값이 나온다.
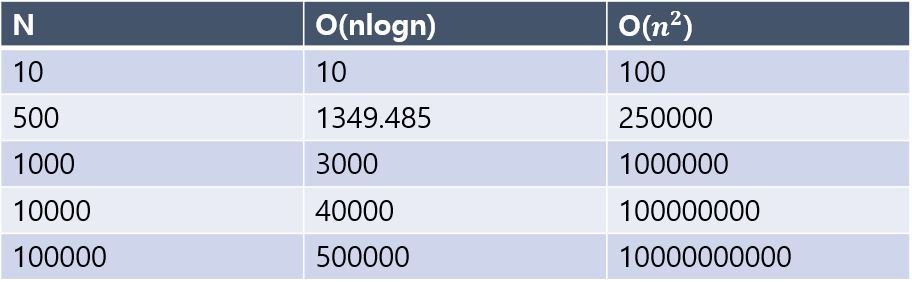
N 크기의 DFT를 짝수번째 항과 홀수번째 항으로 나누어 짝수번째 항들의 DFT와 홀수번째 항들의 DFT를 합치면 O(nlogn)이 된다.
 이미지: PPT캡쳐
이미지: PPT캡쳐1
2
3
4
5
6
7
8
9
10
11
12
13
14
import numpy as np
def fft(x):
N = len(x) # 파라미터 리스트의 길이
even = fft(x[0::2]) # 짝수 항 0부터 2간격
odd = fft(x[1::2]) # 홀수 항 1부터 2간격
T = [np.exp(-2j*np.pi*k/N)*odd[k] for k in range(N//2)] # 홀수항과 회전인자 곱
# 합치기
return [even[k] + T[k] for k in range(N//2)] + \
[even[k] - T[k] for k in range(N//2)]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
import numpy as np
from matplotlib import pyplot as plt
from pylab import rcParams
rcParams['figure.figsize'] = 11, 10 # 그래프를 나타낼 창의 크기 설정
def fft(x):
# FFT 사용자 함수 정의
N_len = len(x) # 파라미터 리스트의 길이
if N_len <= 1:
return x
even = fft(x[0::2]) # 짝수 항 0부터 2간격
odd = fft(x[1::2]) # 홀수 항 1부터 2간격
T = [np.exp(-2j*np.pi*k/N_len)*odd[k]
for k in range(N_len//2)] # 홀수 항과 회전인자의 곱
# 합치기
T_sum = [even[k] + T[k] for k in range(N_len//2)] + \
[even[k] - T[k] for k in range(N_len//2)]
return T_sum
fs = 512 # 샘플링 주파수
dt = 1/fs # 샘플링 주기
N = 512 # 데이터 길이
t = np.arange(0, 1, 1/fs) # 0 <= t <= 1, step
# 입력 신호
r = 3 * np.cos(2 * np.pi * 10 * t) + 6 * \
np.sin(2 * np.pi * (15 * t - 3/8*pow(np.pi, 2)))
x_list = list(r) # 입력신호 type list로 변경
x_fft = fft(x_list) # 입력신호 FFT함수에 입력
# 변환된 그래프가 그려질 주파수 범위 설정
f = np.arange(0, N)
# Original Signal 그래프 나타내기
plt.subplot(211)
plt.title('Original Signal x(t)') # title of graph
plt.xlabel('time') # x축 label
plt.plot(t, r)
# 변환된 그래프 나타내기
plt.subplot(212)
plt.title('Fast Fourier Transform Graph X(f)') # title of graph
plt.xlabel('frequency') # x축 label
plt.plot(f[0: int(N//20)], x_fft[0:int(N//20)])
plt.savefig('./img/fast_fourier.png') # 사진으로 저장하기
plt.show()
아래 그림은 주어진 식의 그래프와 푸리에 변환된 그래프이다.
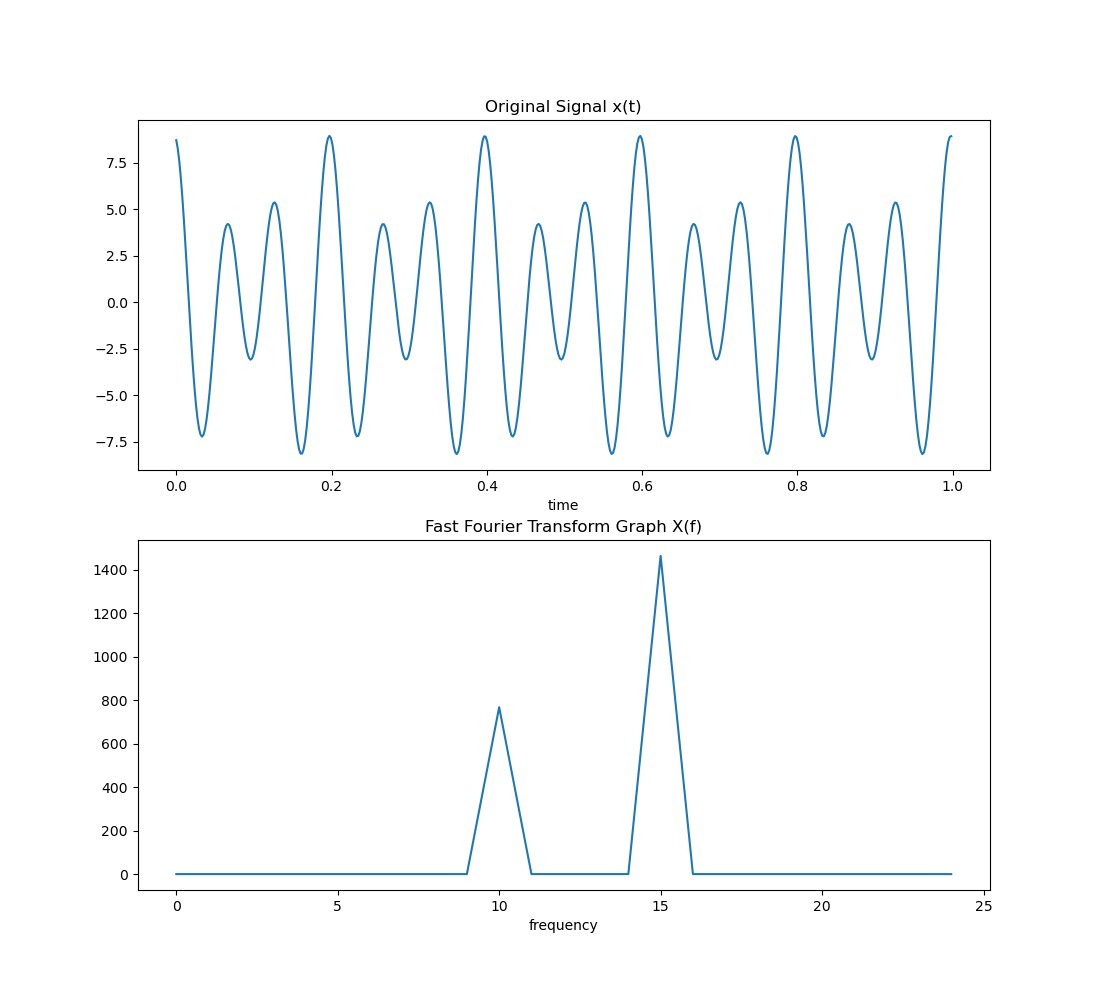
변환된 그래프에서 입력 신호의 스펙트럼을 알 수 있다. Peak 주파수가 10, 15이다.주어진 식에서 cos함수와 sin함수의 주파수가 각각 10, 15 인것을 생각하면 알맞게 변환된 것을 알 수 있다.
FFT(고속 푸리에 변환)에 대해 알아보았다. DFT(이산 푸리에 변환)과 FFT(고속 푸리에 변환)을 비교해 보며 시간 복잡도가 큰 역할을 한다는 것을 알게 되었다.
실제로 푸리에 변환을 사용하게 된다면 방대한 데이터를 다룰 것이기 때문에 고속 푸리에 변환은 중요하다고 생각한다. 예를들어 푸리에 변환은 푸리에 급수와 다르게 비주기 함수도 변환이 가능하다는 장점을 이용해 창업자가 가게를 내고 싶은 지역의 유동인구를 그래프화 한 다음 푸리에 변환을 통해 유동인구가 많은 시간이나 연령대를 알기 쉬울것 같다고 생각한다.
항상 어렵다고 생각했던 것들이 우리에게 많은 도움을 주고, 다양한 형태로 사용될 수 있다고 느꼈다.