Perceptron

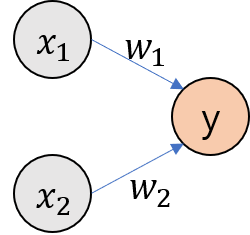
• 여러개의 신호를 입력으로 받아 하나의 신호로 출력한다.
• $x_1$ 과 $x_2$는 입력 신호 , y는 출력 신호, $w_1$과 $w_2$는 가중치를 나탄낸다.

\begin{align} y = 0 & (w_1x_1 + w_2x_2 <= \theta) \end{align}

\begin{align} y = 1 & (w_1x_1 + w_2x_2 > \theta) \end{align}

• 각각의 입력 신호와 가중치들의 곱을 합한 값이 임계값$\theta$를 넘으면 1을 출력한다.
• 가중치가 클수록 해당 입력이 중요하다는 것을 알 수 있다.

How to learn perceptron

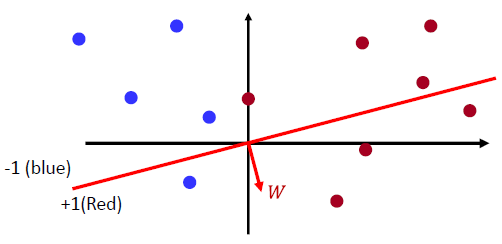
• 초기에는 랜덤하게 normal vector W를 초기화 한다.

Classification rule $sign(W^TX)$

• W벡터와 같은 방향은 +1 클래스로 분류되고, W벡터와 반대편은 -1 클래스로 분류된다.
• 아래의 파란점은 잘못 분류되었으므로 W벡터를 업데이트 해줘야 한다.

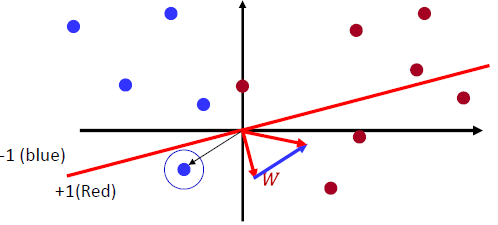
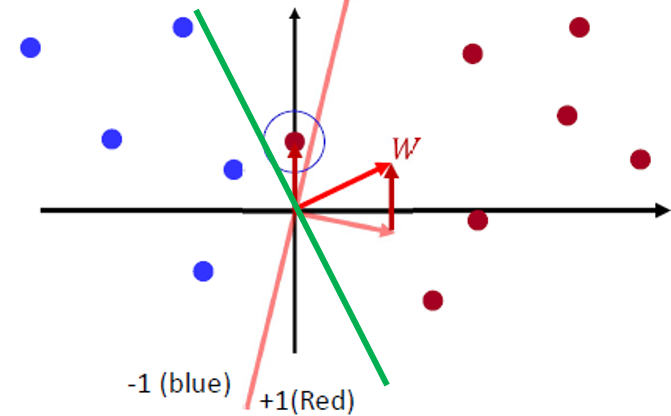
• 두 번의 W벡터 업데이트를 통해 완벽하게 파란점과 빨간점을 분류할 수 있다.

Perceptron with added weight

• 편향(bias)가 추가된 퍼셉트론은 아래와 같다.

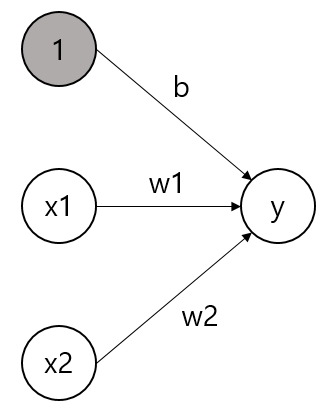
• $x_1$, $x_2$, 3개의 신호가 뉴런에 입력되어 다음 뉴런에 전달된다.
• 다음 뉴런에서는 3개의 신호들의 합이 0을 넘으면 1을 출력하고, 그렇지 않으면 0을 출력한다.

\begin{align} y = h(b + w_1x_1+w_2x_2) \end{align}

\begin{align} h(x) = 0&(x<=0) \end{align}

\begin{align} h(x) = 1&(x>0) \end{align}

• 입력 신호들의 총합이 h(x)함수를 거쳐 변환된 값이 y의 출력이 된다.
• h(x)함수는 입력이 0을 넘으면 1을 반환하고, 그렇지 않으면 0을 반환한다.

Activation Function

• 위에서 h(x)와 같은 함수를 ‘활성함수’라고 한다.
• 입력된 신호들의 총 합이 활성화를 일으키는지 정의하는 역할을 해준다.
• Step function(계단 함수)라고도 한다.

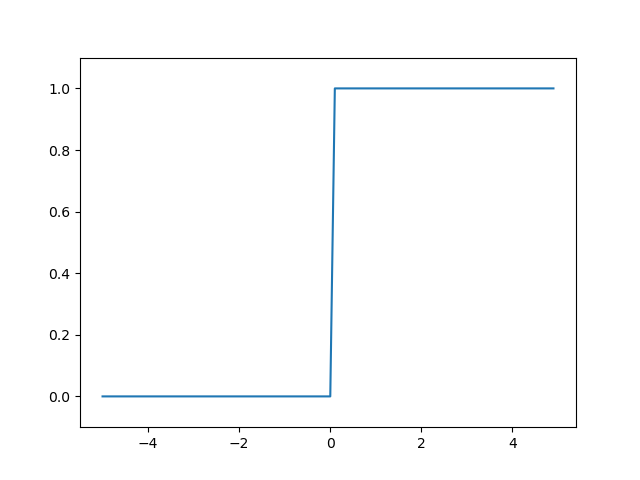
Step Function

• -5.0에서 5.0까지의 간격이 0.1인 numpy배열을 생성한다.
• 배열의 원소를 입력으로 계단함수를 실행하여 다시 배열로 만들어 그래프를 그려준다.

1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
import matplotlib.pylab as plt

def step_function_np(x):
    y = x > 0
    return y.astype(np.int)

x = np.arange(-5.0, 5.0, 0.1)
y = step_function_np(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

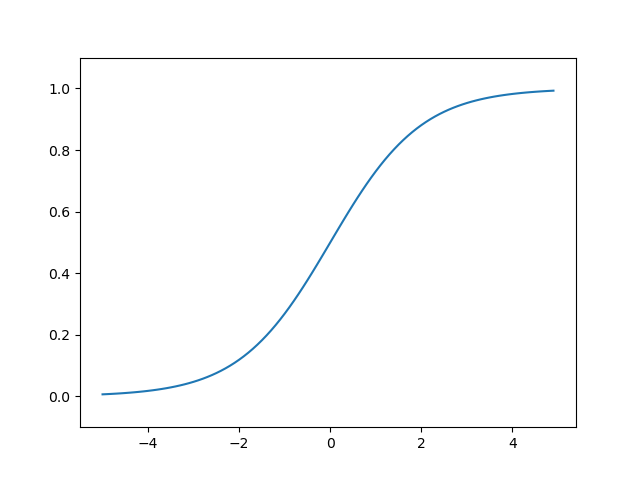
Sigmoid Function

• 시그모이드 함수는 계단함수보다 부드러운 함수이다.
• 출력이 연속적으로 변한다.

\begin{align} h(x) = 1 / 1+\exp(-x) \end{align}

1
2
3
4
5
6
7
8
9
10
11
import numpy as np
import matplotlib.pylab as plt

def sigmpoid(x):
    return 1 / (1 + np.exp(-x))

x = np.arange(-5.0, 5.0, 0.1)
y = sigmpoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

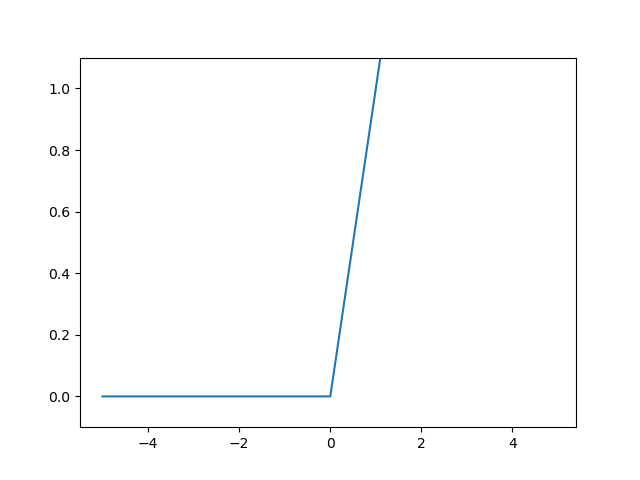
ReLU Function

• ReLU함수는 입력이 0을 넘으면 입력을 그대로 출력하고, 그렇지 않으면 0을 출력하는 활성함수이다.
• maximum함수는 두 입력값 중 큰 값을 반환한다.

\begin{align} h(x) = x &(x>0) \end{align}

\begin{align} h(x) = 0 &(x<=0) \end{align}

1
2
3
4
5
6
7
8
9
10
11
import numpy as np
import matplotlib.pylab as plt

def ReLU(x):
    return np.maximum(0, x)

x = np.arange(-5.0, 5.0, 0.1)
y = ReLU(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

References

_{강의: CMU Introduction to Deep Learning
코드: 밑바닥부터 시작하는 딥러닝}