Derivative

• 미분은 한 순간의 변화량을 표현한 것이다.

  

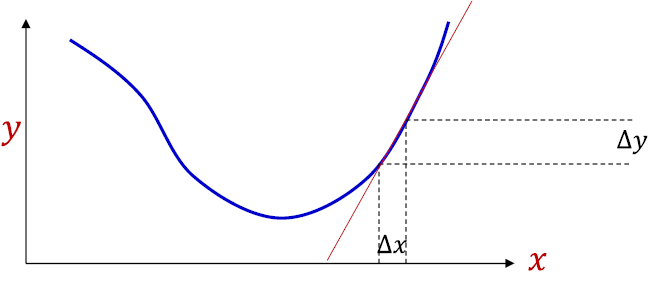
  \begin{align} \Delta y = \alpha \Delta x \end{align}

  • $\alpha$(기울기)와 x변화량의 곱은 y의 변화량과 같다.
  • 일반적인 최적화 문제는 f(x)의 값이 가장 작아지거나 가장 커지는 x를 찾는 것이다.

Gradient Descent

• 기울기를 이용하여 함수의 최솟값이나 최댓값을 찾는다.
• 함수가 볼록한 형태에서는 항상 경사 하강법으로 최솟값을 찾을 수 있다. (a)

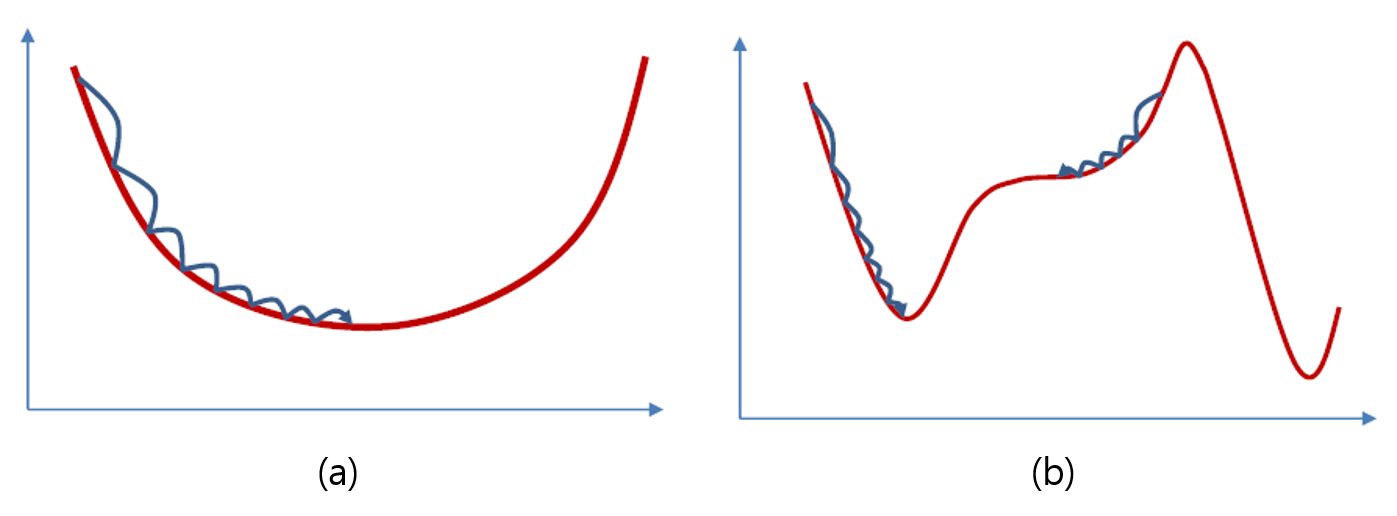
• 볼록하지 않은 함수에서는 해당 함수의 극솟값이나 안정점에 도달 할 수 있다. (b)

  

  경사법에 의한 $f(x_0, x_1) = (x_0)^2 + (x_1)^2$ 함수의 갱신 과정

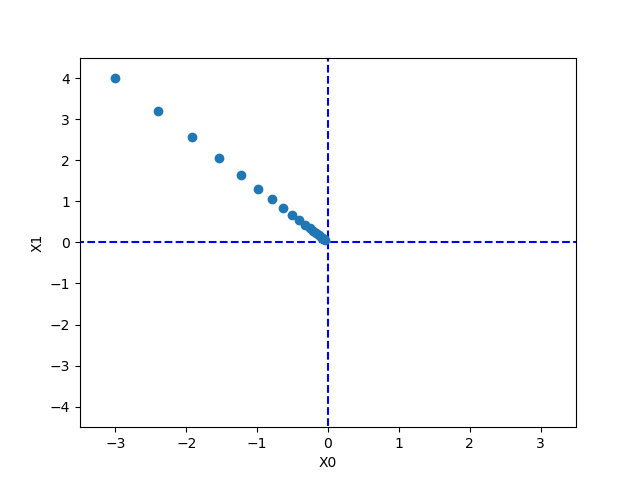
  \begin{align} x_0 = \eta ({\partial f / \partial x_0}) \end{align}

  • $\eta$는 갱신하는 양을 나타낸다. 학습률(learning rate)이다.
  • numerical_gradient 함수는 함수의 기울기를 반환해 준다.
  • gradient_descent 함수에서 init_x는 초기값, lr은 learning rate, step_num은 경사법에 따른 반복 횟수다.
  • function_2는 함수 $f(x_0,x_1)$이다.

  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16
  17
  18
  19
  20
  21
  22
  23
  24
  25
  26
  27
  28
  29
  30
  31
  32
  33
  34
  35
  36
  37
  38
  39
  40
  41
  42
  43
  44
  45
  46
  47
  48
  49
  50
  51
  52
  import numpy as np
  import matplotlib.pylab as plt
  
  def numerical_gradient(f, x):
      h = 1e-4
      grad = np.zeros_like(x)
  
      for idx in range(x.size):
          tmp_val = x[idx]
  
          # f(x+h)
          x[idx] = tmp_val + h
          fxh1 = f(x)
  
          # f(x-h)
          x[idx] = tmp_val - h
          fxh2 = f(x)
  
          grad[idx] = (fxh1 - fxh2) / (2 * h)
          x[idx] = tmp_val
      return grad
  
  def gradient_descent(f, init_x, lr=0.01, step_num=100):
      x = init_x
      x_history = []
  
      for i in range(step_num):
          x_history.append(x.copy())
  
          grad = numerical_gradient(f, x)
          x -= lr * grad
  
      return x, np.array(x_history)
  
  def function_2(x):
      return x[0] ** 2 + x[1] ** 2
  
  init_x = np.array([-3.0, 4.0])
  
  lr = 0.1
  step_num = 20
  x, x_history = gradient_descent(function_2, init_x, lr=lr, step_num=step_num)
  
  plt.plot([-5, 5], [0, 0], '--b')
  plt.plot([0, 0], [-5, 5], '--b')
  plt.plot(x_history[:, 0], x_history[:, 1], 'o')
  
  plt.xlim(-3.5, 3.5)
  plt.ylim(-4.5, 4.5)
  plt.xlabel("X0")
  plt.ylabel("X1")
  plt.show()
  

  

  • 경사법을 사용한 갱신 과정을 나타낸 그림으로 최솟값인 원점에 점점 가까워지는 것을 볼 수 있다.

Softmax Function

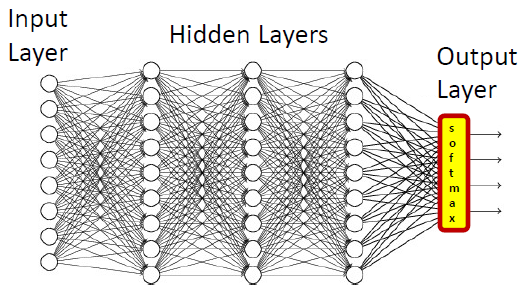
\begin{align} {y_k} = \exp(a_k) / {\sum{^n}}_{i=1} {\exp(a_i)} \end{align}

• n은 출력층의 뉴런 수, $y_k$는 그중 k번째 출력을 뜻한다.
• softmax 함수는 분류해야 하는 클래스의 총 개수를 a라고 할 때 b차원의 벡터를 입력 받아 각 클래스에 대한 확률을 추정한다

1
2
3
4
5
6
7
8
# softmax function
def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a

    return y

1
2
3
4
5
6
7
8
np.array([0.3, 2.9, 4.0])
# array([0.3, 2.9, 4. ])

softmax(a)
# array([0.01821127, 0.24519181, 0.73659691])

np.sum(res)
# 1.0

• softmax 함수의 출력은 0과 1사이의 실수다.
• softmax 함수의 출력의 총합은 1이다.

References

_{강의: CMU Introduction to Deep Learning
코드: 밑바닥부터 시작하는 딥러닝}