Chain Rule

\begin{align} y = f(g(x)) \end{align}

\begin{align} {dy / dx} = {df / dg(x)} {dg(x) / dx} \end{align}

• Chain Rule은 합성함수의 미분을 위한 공식이다.

$z = g(x)$, $y = f(z)$라고 가정한다면

\begin{align} \Delta z = {dg(x) / dx} \Delta x \end{align}

\begin{align} \Delta y= {df / dz} \Delta z= {df / dg(x)} {dg(x) / dx} \Delta x \end{align}

• $dg(x)$가 약분이 되면서 아래 식처럼 되는것을 확인할 수 있다.

  \begin{align} \Delta y={dy / dx} \Delta x \end{align}

  

• z에 대한 y의 미분은 x에 대한 g(x)의 편미분들의 합이 된다.

Jacobian

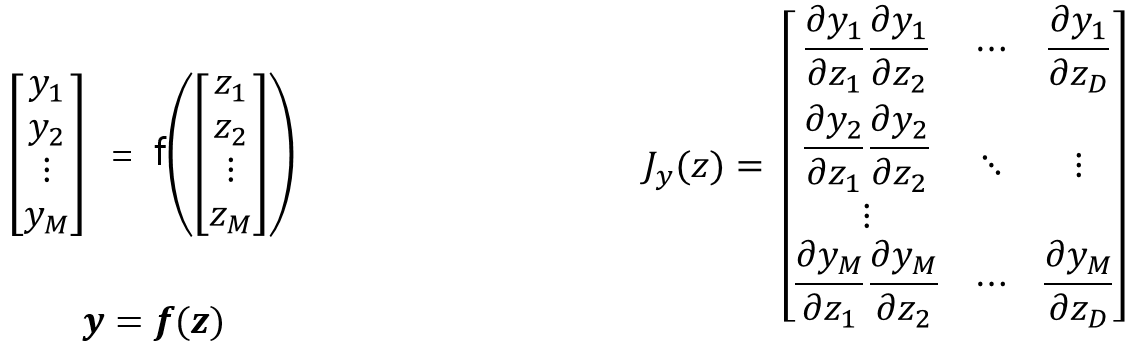
\begin{align} \Delta y = J_y (z) \Delta z \end{align}

• 벡터 입력에 대한 벡터 함수의 미분이 Jacobian행렬이다.
• 열 벡터 y를 미분하면 z에 대한 y의 편미분인 Jacobian 행렬과 z의 미분의 곱으로 나타낼 수 있다.
• 함수 $f$가 스칼라인 경우는 y의 Jacobian 행렬이 대각 행렬이다.
• 함수 $f$가 벡터인 경우는 y의 Jacobian 행렬이 전체 행렬이다.

Forward propagation using scalar formula

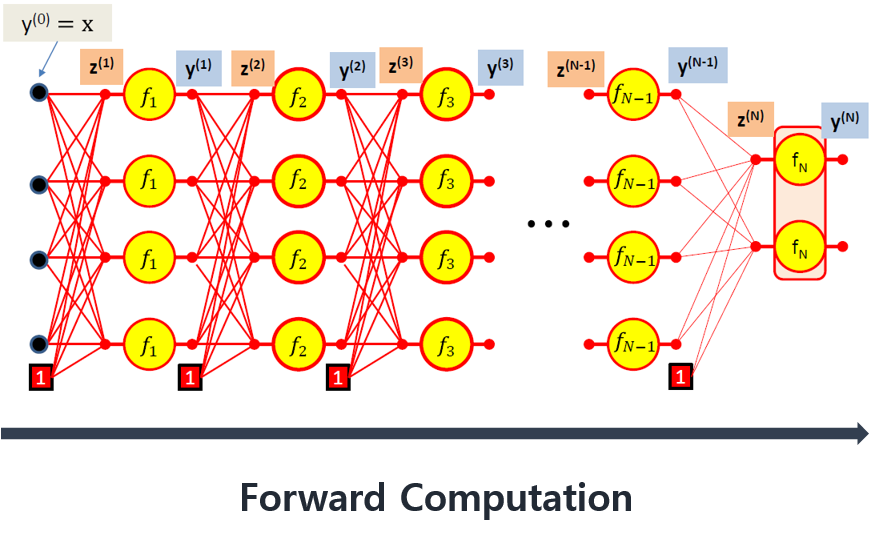
\begin{align} {z_j}^{(n)} = {\sum}_i {w_{ij}}^{(N)}{y_i}^{(N-1)} \end{align}

\begin{align} {y_j}^{(N)} = f_{N({z_j}^{(N)})} \end{align}

• 신경망에서의 순전파는 입력층에서 은닉층 방향으로 이동한다
• 각각의 입력에 대한 가중치가 곱해지고 가중치의 합으로 계산된 후 각 은닉층 뉴런의 함수를 거쳐 다음 은닉층의 입력으로 전달되어 최종 결과를 출력한다.

Backward propagation using scalar formula

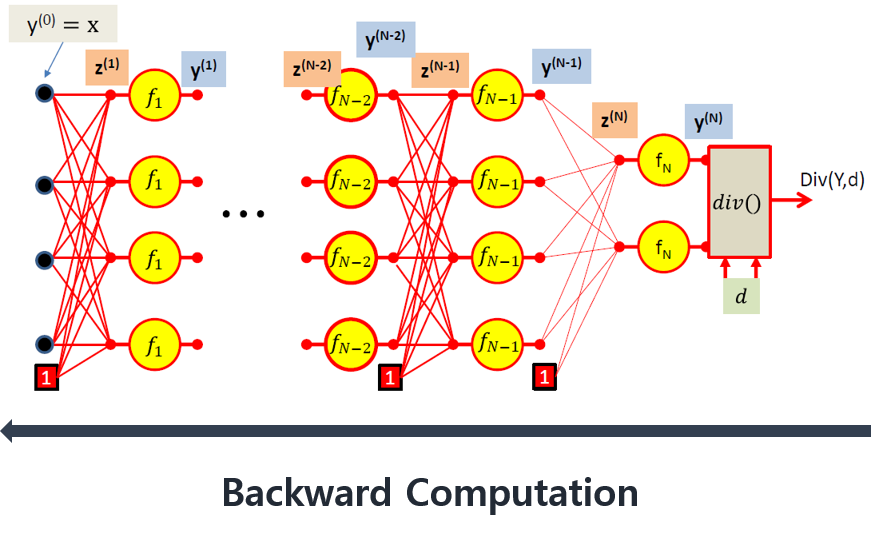
• 역전파의 시작은 divergence(Div)를 미분하는것으로 시작한다. \begin{align} \color{orange}{\partial Div(Y,d) / \partial {y_i}^{(N)}} \color{black}= \partial Div(Y,d)/\partial y_i \end{align}

• Output layer 부분에서 y에 대한 divergence의 편미분은 단순한 미분형태이다.

\begin{align} \color{black}\partial Div/\partial {z_1}^{(N)} = \color{blue}\partial {y_1}^{(N)}/\partial {z_i}^{(N)}\color{black}* \color{orange}{\partial Div / \partial {y_i}^{(N)}} \end{align}

\begin{align} \color{blue}\partial {y_1}^{(N)}/\partial {z_i}^{(N)} \color{black}= {f_N}’({z_1}^{(N)}) \end{align}

\begin{align} \color{red}\partial Div/\partial {z_1}^{(N)}={f_N}’({z_1}^{(N)})*\partial Div / \partial {y_i}^{(N)} \end{align}

• z에 대한 Div의 편미분이다.
• y에 대한 Div의 편미분은 앞에서 계산되었고 z에 대한 y의 편미분은 활성함수를 미분하는것과 같다.

\begin{align} \color{black}\partial Div/\partial {w}_{11^{(N)}} = \color{orange}\partial {w_{11}}^{(N)}/\partial {z_1}^{(N)}\color{black}* \color{blue}{\partial Div / \partial {z_1}^{(N)}} \end{align}

\begin{align} \color{orange}\partial {w_{11}}^{(N)}/\partial {z_1}^{(N)} \color{black}={y_1}^{(N-1)} \end{align}

\begin{align} \color{red}\partial Div/\partial {w_{11}}^{(N)} = {y_1}^{(N-1)}* \partial Div / \partial {z_1}^{(N)} \end{align}

• 가중치 w에 대한 Div 편미분이다.
• z에 대한 Div의 편미분은 앞에서 계산되었고 $z = wy +b$이기 때문에 가중치에 대한 z의 편미분은 y가 된다.

\begin{align} \partial Div/\partial {y_{1}}^{(N-1)} = {\sum}_i {\color{orange}\partial {z_{j}}^{(N)}/\partial {y_1}^{(N-1)} \color{black}* \color{blue}\partial Div/\partial {z_j}^{(N)}} \end{align}

\begin{align} \color{orange}\color{orange}\partial {z_{j}}^{(N)}/\partial {y_1}^{(N-1)} \color{black}={w}_{1j^{(N)}} \end{align}

\begin{align} \color{red}\partial Div/\partial {y_{1}}^{(N-1)} = {\sum}_i {w}_{1j^{(N)}}*\partial Div/\partial {z_j}^{(N)} \end{align}

• 은닉층에서의 y에 대한 Div의 편미분이다.
• Output layer에서와의 차이점은 y에 대한 z의 편미분이 있다는 것이다.
• $z = wy+b$인 것을 생각하면 y에 대한 z의 편미분은 w가 되는것을 알 수 있다.

Forward propagation using vector formula

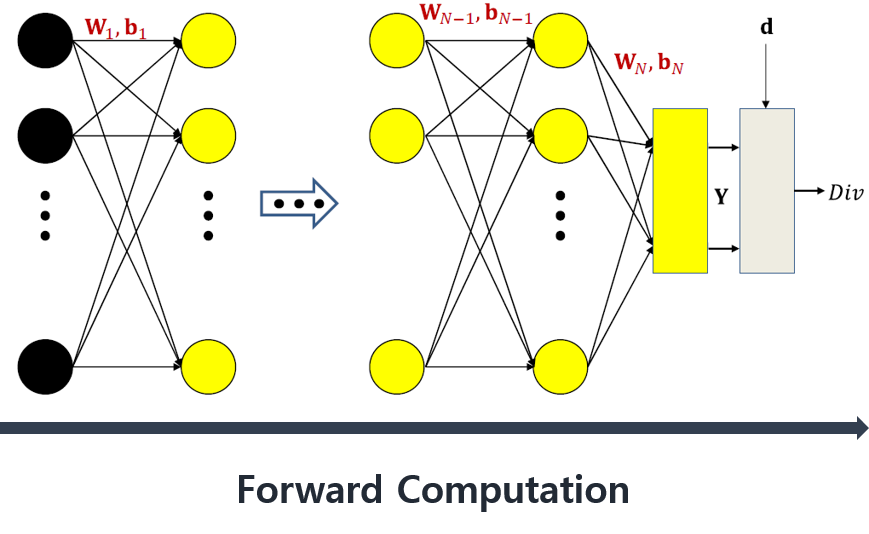
\begin{align} z_k = W_k {y}_{k-1} + b_k \end{align}

\begin{align} y_k = f_k(z_k) \end{align}

\begin{align} Y = {f}_N(W_N{f}_{N-1}(…f_2(W_2f_1(W_1x+b_1)+b_2)…+b_N) \end{align}

• 입력 x, z(wy+b), 레이어 출력 y, 편향 b는 열 벡터이고, 가중치 w는 행렬이다.
• z는 가중치와 입력의 곱과 편향의 합이다.
• 식 $Y$는 입력층부터 마지막 레이어까지 전파된 출력이다.

Backward propagation using vector formula

• 역전파는 Y에 대한 Div의 편미분으로 시작된다.

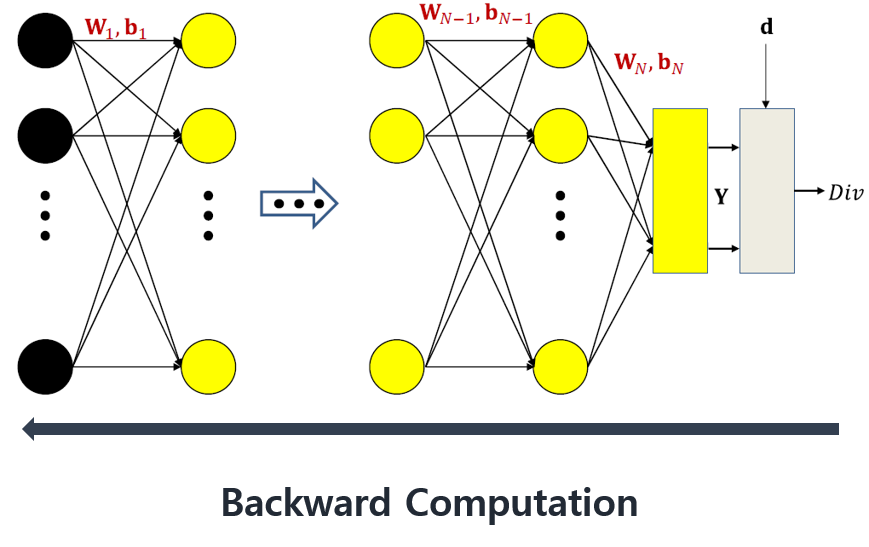
\begin{align} \color{blue}{\nabla _YDiv} \end{align}

\begin{align} \nabla_{z_N}Div = \color{blue}{\nabla_YDiv}\color{orange}{\nabla_{z_N}Y} \end{align}

\begin{align} \color{orange}{\nabla_{z_N}Y }\color{black}= J_Y(Z_N) \end{align}

\begin{align} \color{red}{\nabla_{z_N}Div = {\nabla_YDiv}J_Y(Z_N)} \end{align}

• Z에 대한 Div의 편미분이다.
• Y에 대한 Div의 편미분은 앞에서 계산되었고, chain rule과 Jacobian에 의하면 Y의 Jacobian행렬이 나온다.

\begin{align} \nabla_{y_{N-1}}Div = \color{blue}{\nabla_z{_N}Div}\color{black}*\color{orange}{\nabla_{y{_N-1}}Z_N} \end{align}

\begin{align} \color{orange}{\nabla_{y_{N-1}}Z_N }\color{black}= W_N \end{align}

\begin{align} \color{red}{\nabla_{y_{N-1}}Div = \nabla_z{_N}Div*W_N} \end{align}

• 은닉층에서 y에 대한 Div의 미분은 output layer와 차이가 있다.
• Z에 대한 Div의 편미분은 앞에서 계산되었고, y에 대한 Z의 편미분은 W로 나타낼 수 있다.

\begin{align} \nabla_{w_{k}}Div = y_{k-1}* \nabla_{z_{k}}Div \end{align}

\begin{align} \nabla_{b_{k}}Div = \nabla_{z_{k}}Div \end{align}

• 가중치와 편향에 대한 Div의 편미분은 신경망 학습에서 가중치, 편향 업데이트에 사용된다.

Neural network training algorithm

• Initialize weights, bias (가중치 편향 초기화)

• DO:

  $Loss = 0$

  For all k, initialize $\nabla_{w_k}Loss = 0, \nabla_{b_k}Loss = 0$

  For all t = 1:T

  • Forward propagation:

    Output$Y(X_t$)

    Divergence $Div(Y_t,d_t)$

    $Loss +=Div(Y_t, d_t)$

  • Backward propagation

    $\nabla_{y_{k}}Div = {\nabla_{Z_{k+1}}Div}W_{k+1}$

    $\nabla_{z_{k}}Div = {\nabla_{y_{k}}Div}J_{y_k}(z_k)$

    $\nabla_{w_k}Div = y_{k-1}\nabla_{z_k}Div$

    $\nabla_{b_k}Div = \nabla_{z_k}Div$

    $\nabla_{W_k}Loss +=\nabla_{w_k}Div$

    $\nabla_{b_k}Loss +=\nabla_{b_k}Div$

  For all k, update:

  $W_k = W_k {-{\eta / T}(\nabla_{W_k}Loss)^T}$

  $b_k = b_k {-{\eta / T}(\nabla_{W_k}Loss)^T}$

• Until Loss has converged

References

_{강의: CMU Introduction to Deep Learning}