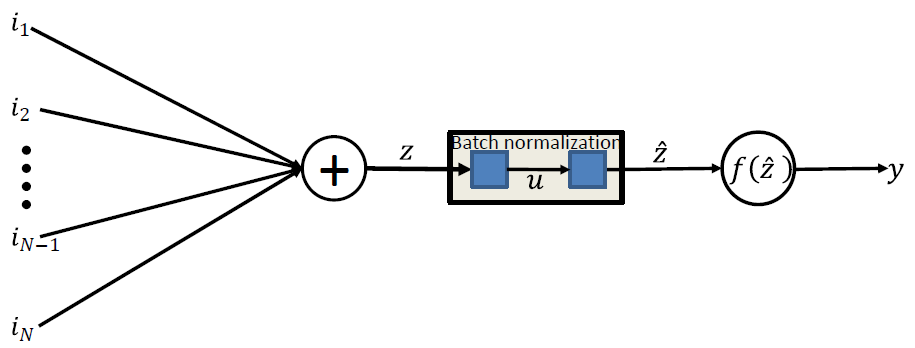
학습 과정을 전체적으로 안정적이게 하여 학습 속도를 높여주는 Batch Normalization을 사용할 수 있다.
Batch Normalization
\begin{align} W \leftarrow W-\eta ({\partial L / \partial W}) \end{align}
1
2
3
4
5
6
7
class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params, grads:
params[key] -= self.lr * grads[key]
\begin{align} v \leftarrow \alpha v - \eta ({\partial L / \partial W}) \end{align}
\begin{align} W \leftarrow W+v \end{align}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
params[key] += self.v[key]
\begin{align} h \leftarrow h+{\partial L / \partial W} \odot {\partial L / \partial W} \end{align}
\begin{align} W \leftarrow W-\eta ({1 / {\sqrt {h}}})*({\partial L / \partial W}) \end{align}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class AdaGrad:
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
\begin{align} E[{\partial {_w}}^{2} D]_k = \gamma E[{\partial {_w}}^{2} D]_{k-1} +(1-\gamma)({\partial {_w}}^{2} D)_k \end{align}
\begin{align} w_{k+1} = w_k - ({\eta / \sqrt{E[{\partial {_w}}^{2} D]_{k+\epsilon}}}) * \partial_wD \end{align}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class RMSprop:
def __init__(self, lr=0.01, decay_rate=0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
\begin{align} {m_t} = {\beta_1} {m}_{t-1}+(1-{\beta_1})g_t \end{align}
\begin{align} v_t = {\beta_2}v_{t-1}+(1-\beta_2){g{_t}}^2 \end{align}
\begin{align} \hat{m}_t = {m_t / 1-{\beta{_1}}^t} \end{align}
\begin{align} \hat{v} = {v_t / 1-{\beta{_2}}^t} \end{align}
\begin{align} \theta_{t+1} = \theta_t-({\eta / \sqrt{\hat{v_t}+\epsilon}}) \hat{m}_t \end{align}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Adam:
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)
for key in params.keys():
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key] ** 2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
학습 과정을 전체적으로 안정적이게 하여 학습 속도를 높여주는 Batch Normalization을 사용할 수 있다.

\begin{align} u_i = {z_i -\mu_B / \sqrt {\sigma{_B}^2 +\epsilon}} \end{align}
\begin{align} \hat {z}_i = \gamma u_i +\beta \end{align}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
# coding: utf-8
import os
import sys
sys.path.append(os.pardir) # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# 오버피팅을 재현하기 위해 학습 데이터 수를 줄임
x_train = x_train[:300]
t_train = t_train[:300]
# weight decay(가중치 감쇠) 설정 =======================
# weight_decay_lambda = 0 # weight decay를 사용하지 않을 경우
weight_decay_lambda = 0.1
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
)
optimizer = SGD(lr=0.01) # 학습률이 0.01인 SGD로 매개변수 갱신
max_epochs = 201
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0
for i in range(1000000000):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
grads = network.gradient(x_batch, t_batch)
optimizer.update(network.params, grads)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("epoch:" + str(epoch_cnt) + ", train acc:" + str(train_acc) + ", test acc:" + str(test_acc))
epoch_cnt += 1
if epoch_cnt >= max_epochs:
break
# 그래프 그리기==========
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
각 층의 뉴런 갯수는 100개, activation function은 ReLU를 사용하였다.
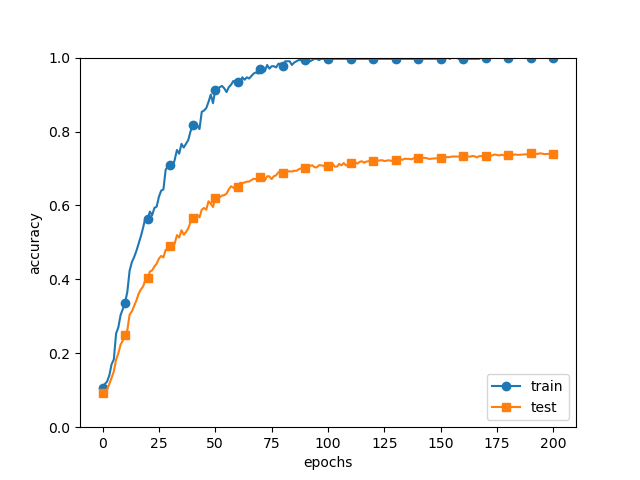
가중치 감소를 추가해 준다.
1
2
3
4
5
6
7
8
9
def loss(self, x, t):
y = self.predict(x)
weight_decay = 0
for idx in range(1, self.hidden_layer_num + 2):
W = self.params['W' + str(idx)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)
return self.last_layer.forward(y, t) + weight_decay
1
2
3
4
5
6
7
8
9
10
11
12
def gradient(self, x, t):
# forward
# backward
# 결과 저장
grads = {}
for idx in range(1, self.hidden_layer_num+2):
grads['W' + str(idx)] = self.layers['Affine' + str(idx)].dW + self.weight_decay_lambda * self.layers['Affine' + str(idx)].W
grads['b' + str(idx)] = self.layers['Affine' + str(idx)].db
return grads
1
2
3
weight_decay_lambda = 0.1
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
weight_decay_lambda=weight_decay_lambda)
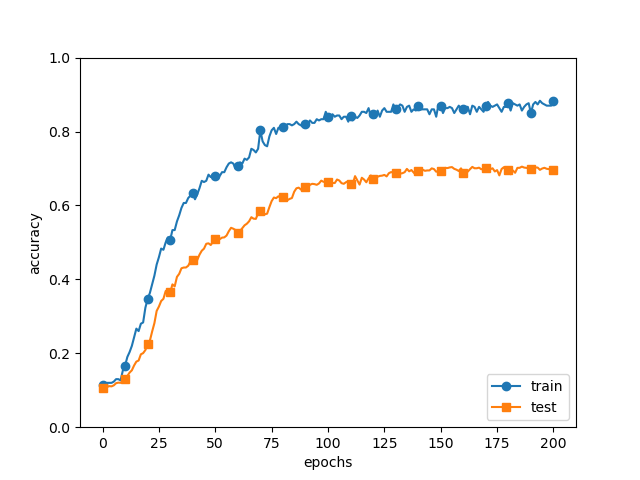
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
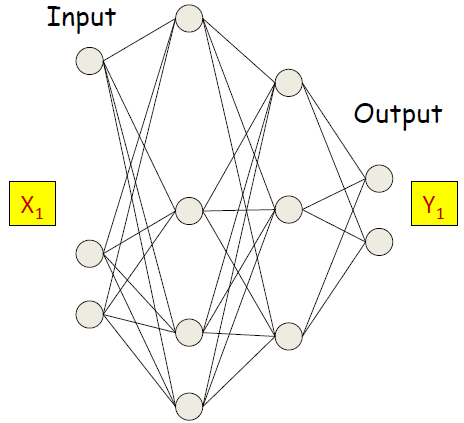
class Dropout:
def __init__(self, dropout_ratio=0.5):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg=True):
if train_flg:
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask
else:
return x * (1.0 - self.dropout_ratio)
def backward(self, dout):
return dout * self.mask
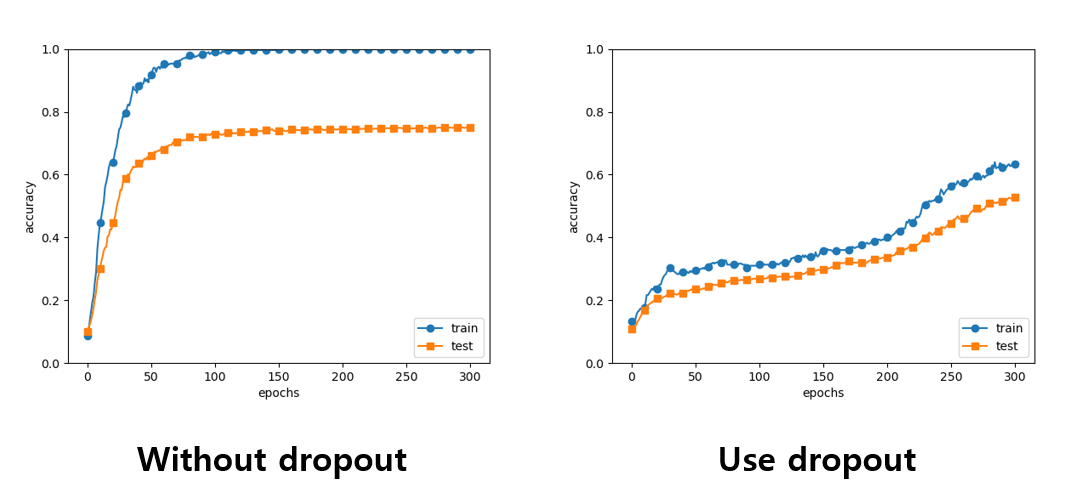
self.mask는 x와 형상이 같은 배열을 무작위로 생성하고 그 값이 0.5(dropout_ratio)보다 큰 원소만 True로 설정한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from common.util import shuffle_dataset
(x_train, t_train), (x_test, t_test) = load_mnist()
# 훈련 데이터를 섞는다
x_train, t_train = shuffle_dataset(x_train, t_train)
# 20%를 검증 데이터로 분할
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]
0단계
하이퍼파라미터 값의 범위를 설정한다
1단계
설정된 범위에서 하이퍼파라미터의 값을 무작위로 추출한다
2단계
1단계에서 샘플링한 하이퍼파라미터 값을 사용하여 학습하고, 검증 데이터로 정확도를 평가한다(epoch은 작게 설정한다.)
3단계
1단계와 2단계를 특정 횟수 반복하여 그 정확도의 결과를 보고 하이퍼파라미터의 범위를 좁힌다
1
2
3
# 탐색한 하이퍼파라미터의 범위 지정
weight_decay = 10 ** np.random.uniform(-8, -4)
lr = 10 ** np.random.uniform(-6, -2)
이 글에 나왔던 common 폴더는 [common] 여기에 있다.