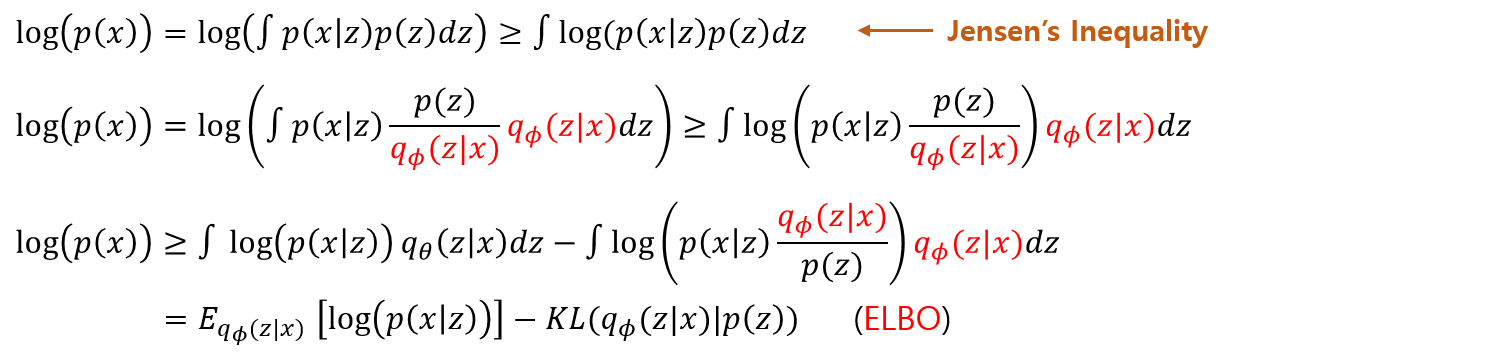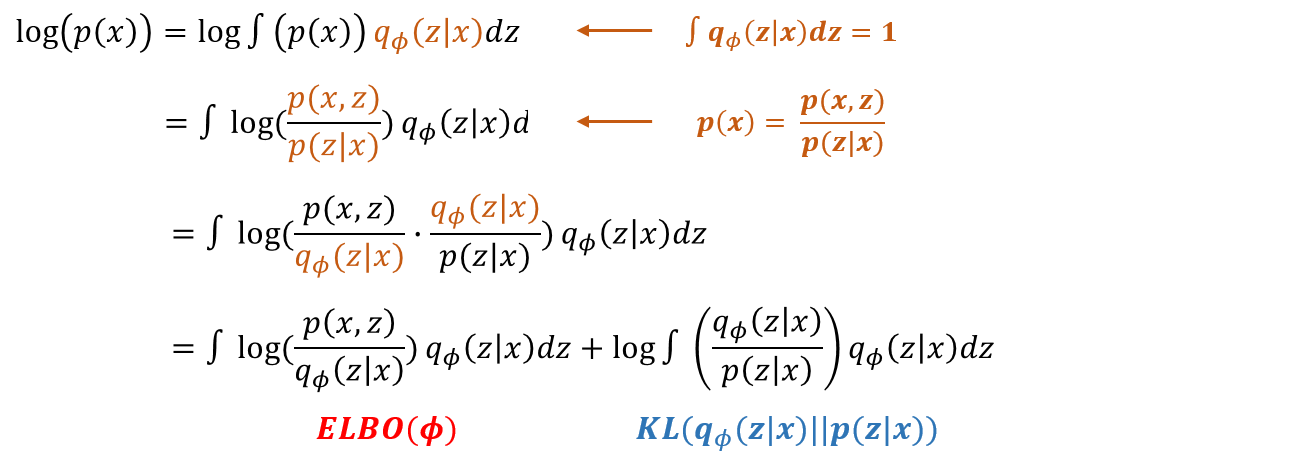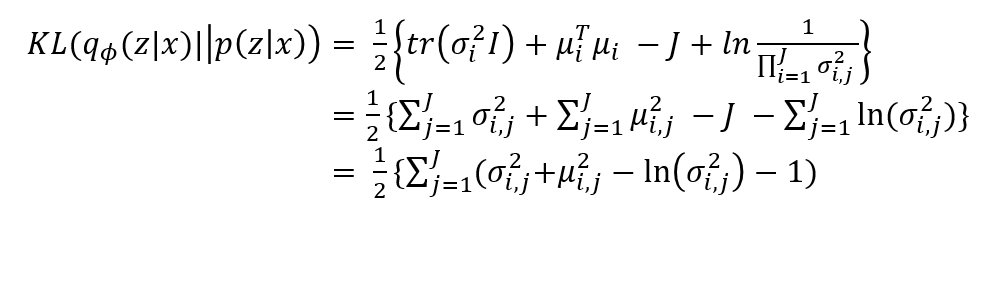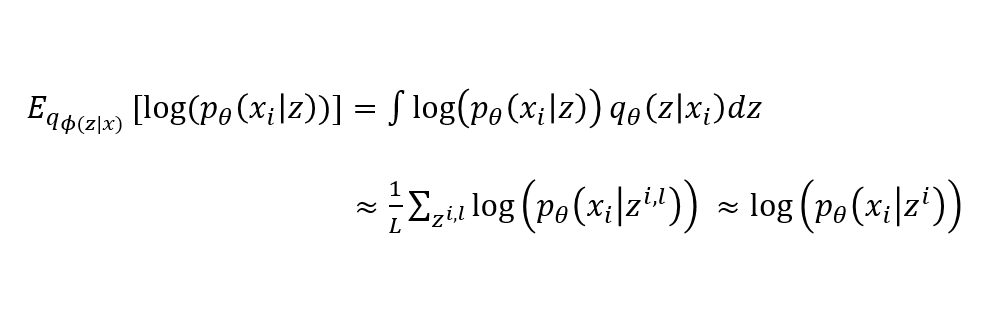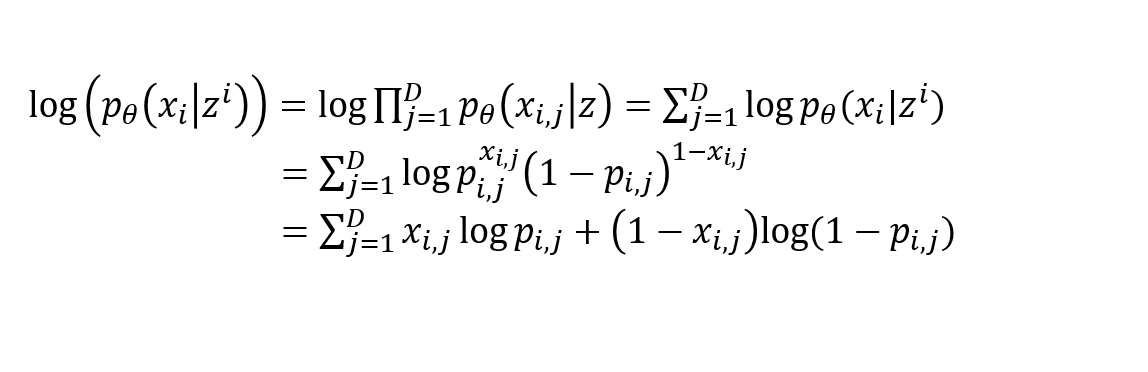Variational Auto Encoder

• Variational auto encoder 는 Generative model 이다.

• Training data의 distribution을 근사하는 특징을 가지고 있다.

  

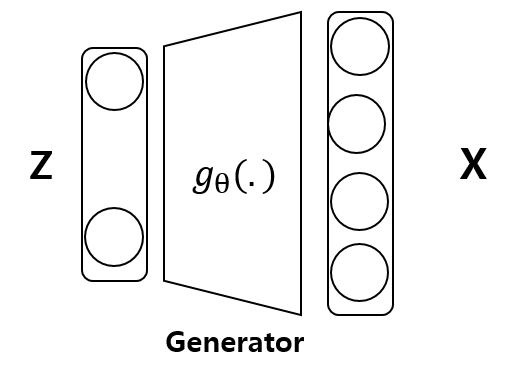
z : latent variable
x : target data

• z~p(z) : random variable
• $g_\theta$(.) : Deterministic function parameterized by $\theta$
• x = g(x) : random variable
• z vector는 controller 역할을 한다. (ex. 사람 얼굴에 화난 얼굴, 기쁜얼굴, 당황한 얼굴 조절 가능)

Intractable calculation issue

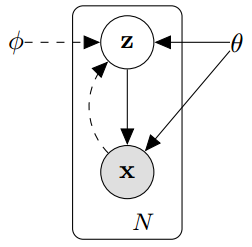
• 실선이 generative model 인 $p_\theta(z)p_\theta(x|z)$이고, 점선은 $q_\theta(z|x)$를 이용해 근사할 $p_\theta(z|x)$이다.
• $p(z|x)$를 계산하기 위한 $p_\theta(x) = \int_z(p_\theta(x|z)p_\theta(z)dz$가 모든 z에 대해 적분 할 수 없기때문에 $q_\theta(z|x)$(입력 x)를 도입하여 계산한다.

Derivation 1

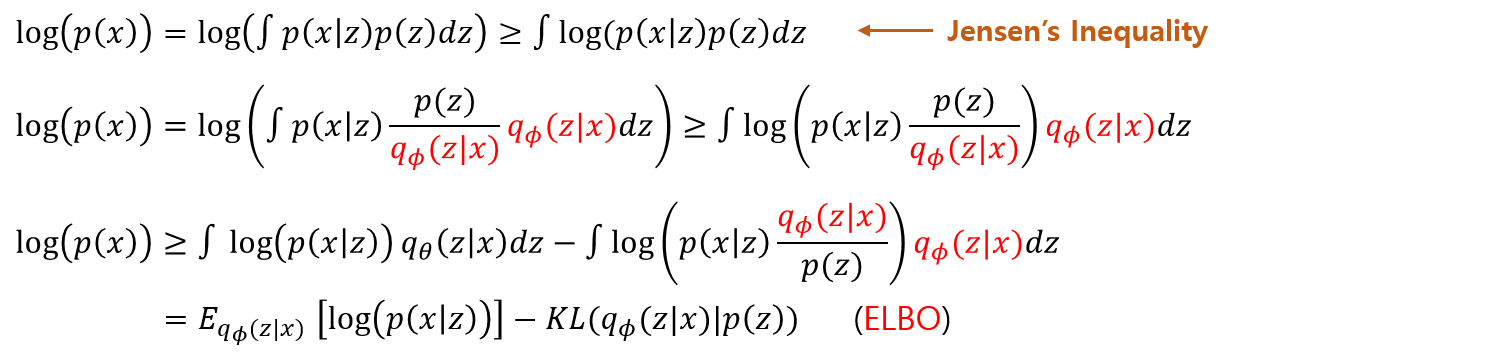
• Concave 함수로 변환하기 위해 log를 씌운다.
• Jensen’s Inequality 를 사용하여 log를 안으로 넣어준다. ($f[E(x)] \ge E[f(x)]$)
• $q{_\phi}(z|x)$를 추가해 준다.
• 최종적으로 정리한 식은 $\log(p(x)$ 보다 작거나 같기 때문에 ELBO(evidence lower bound)라고 한다.

Derivation 2

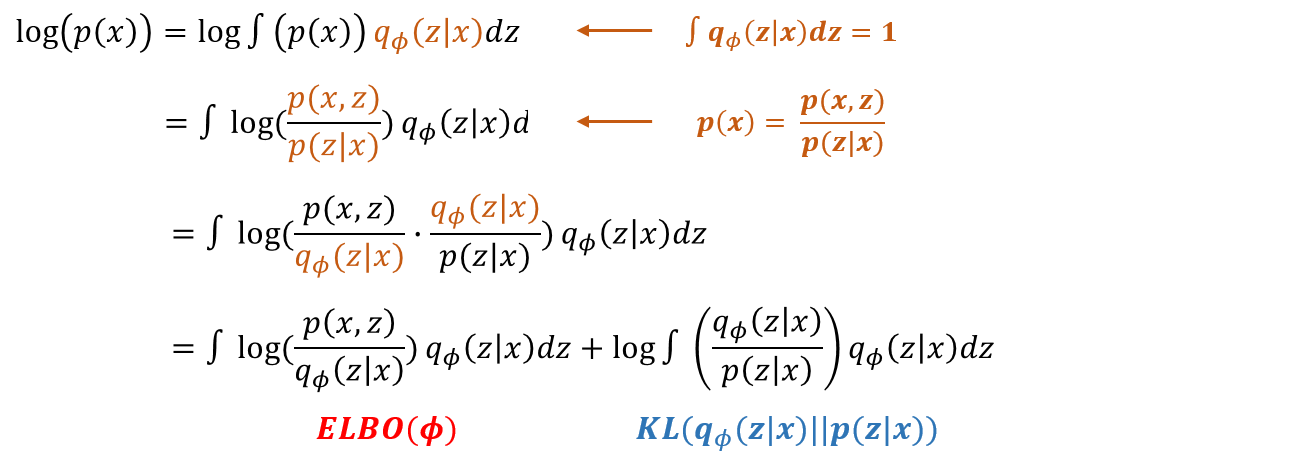
• 2번째 증명 공식은 $p(x) = p(x)$으로 시작 한다.
• z에 대한 확률분포의 모든 합이 1인 것을 이용하여 $p(x)$에 곱해준다.
• 조건부확률의 정의에 따라 $p(x)$를 바꿔준다.
• 증명 1과 같이 $q_\phi (z|x)$를 도입한다.
• 정리된 식의 앞부분은 ELBO와 같고 뒤에 있는 식은 KLD로 나타낼 수 있다.
• KL을 최소화 하는 $q_\theta(z|x)$를 찾으면 되지만 $p(z|x)$를 모르기 때문에 ELBO를 최대화 하는 $\phi$ 값을 찾아야 한다.

LOSS Function

Variational Inference ($\phi$)

\begin{align} \log(p(x)) \ge E_{q{_\phi} (z|x)} [ \log (p(x|z))] - KL(q_\phi(z|x) |p(z)) = ELBO(\phi) \end{align}

Maximum Likelihood ($\theta$)

\begin{align} -{\sum}_i {\log(p(x_i))} \le -{\sum}_i { E_{q{_\phi} (z|x_i)} [ \log (p(x_i|g_\theta(z)))] - KL(q_\phi(z|x) |p(z))} \end{align}

Optimization

\begin{align} argmax_({\phi, \theta}) {\sum}_i -{E_{q{_\phi} (z|x_i)} [ \log (p(x_i|g_\theta(z)))] + KL(q_\phi(z|x_i) |p(z))} \end{align}

• ELBO를 maximize 하는 $\phi, \theta$를 찾는 것이 목표이다.
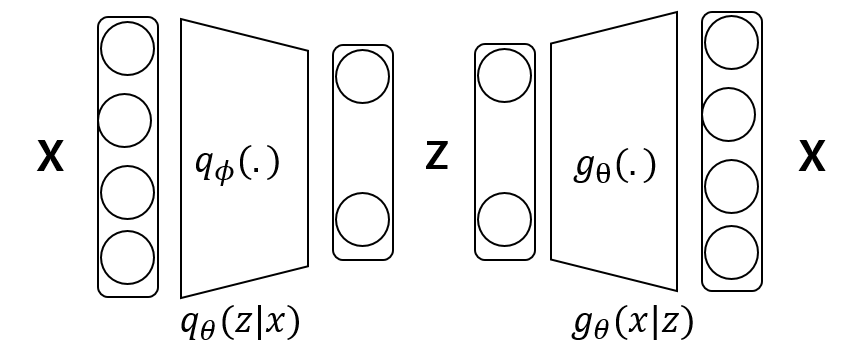
• $q_\theta(z|x)$는 Encoder이고, $g_\theta(x|z)$는 Decoder이다.
• Decoder를 학습시키기위해 Encoder를 도입하였다.

Regularization (Encoder)

• $q_\phi (z|x_i)$는 $N(\mu_i, {\sigma{_i}}^2I)$, $p(z)$는 $N(0,1)$으로 가정한다.

  

두 normal distribution 사이의 KL divergence

• Encoder부분의 계산은 위 식처럼 계산 가능하다.

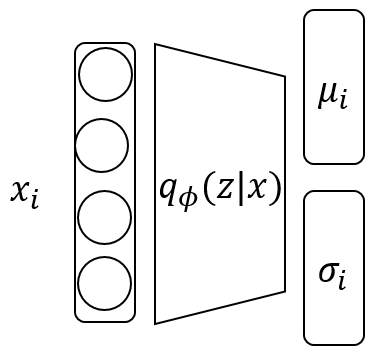
Reparameterization Trick

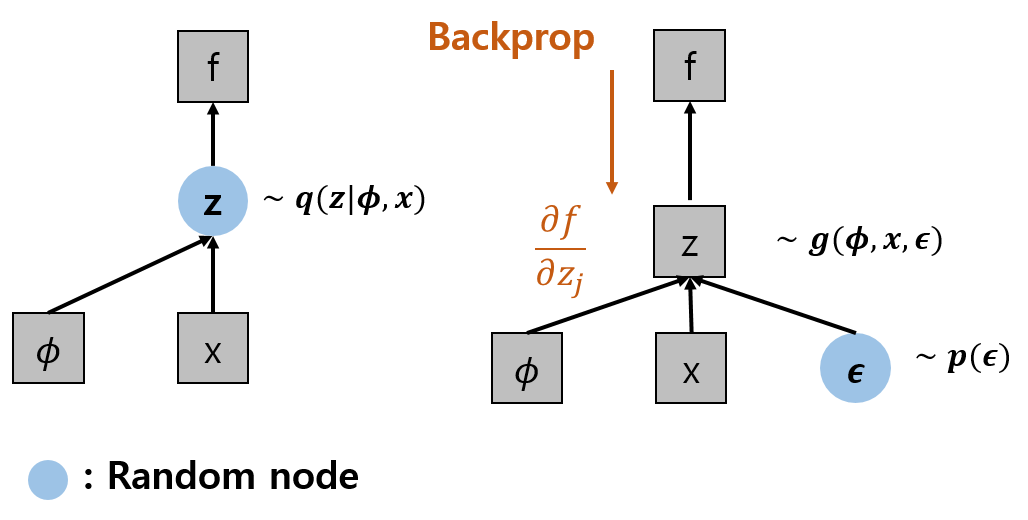
KLD까지 통과를 하고 이제 Decoder 부분으로 넘어가면 되는데 문제가 있다. $q_\theta ()$에서는 sampling을 진행하게 되며, z는 Gaussian distribution이므로 Backpropagation이 불가능하다.

\begin{align} z^{i,j} = \mu_i +{\sigma{_i}}^2 \odot \epsilon \end{align}

• Gaussian distribution인 $z^{i,j}$에 약간의 변형을 준다.
• $\epsilon \sim N(0,I)$이기 때문에 같은 분포지만 Backpropagation이 가능하다.

Reconstruction Error (Decoder)

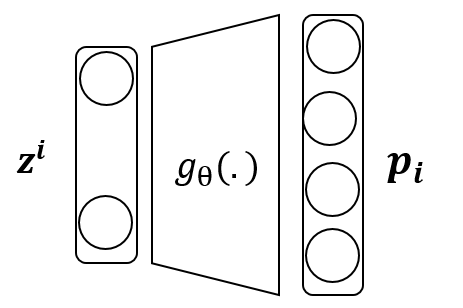
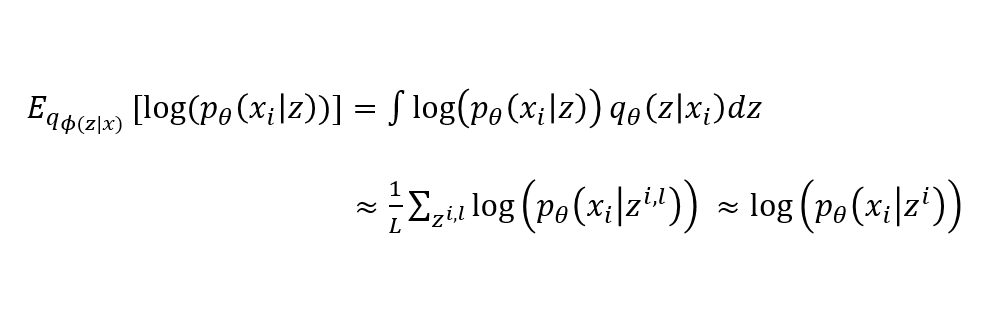
• $L=1$인 경우의 식을 전개하면 아래와 같다.

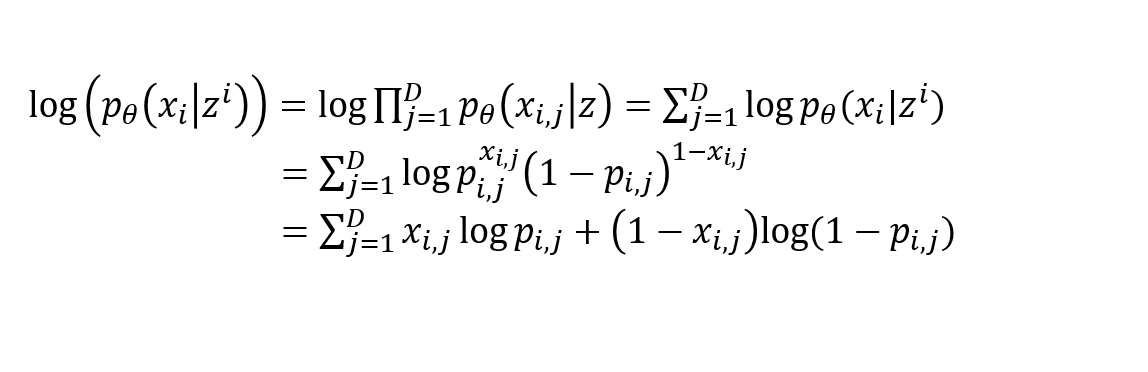
• 입력 x와 출력 $p_{i,j}$ 사이의 cross-entropy가 되는것을 볼 수 있다.

References

오토인코더의 모든 것 - 2/3
ratsgo’s blog