Greedy Algorithm (Python Algorithm interview 21장)

그리디 알고리즘

p.585

• 그리디 알고리즘은 글로벌 최적을 찾기 위해 각 단계에서 로컬 최적의 선택을 하는 휴리스틱 문제 해결 알고리즘이다
• 합리적인 시간 내에 최적에 가까운 답을 찾을 수 있다
• 다이나믹 프로그래밍이 하위 문제에 대한 최적의 솔루션을 찾은 다음, 결과들을 결합한 정보에 입각해 전역 최적 솔루션에 대한 선택을 한다면, 그리디 알고리즘은 각 단계마다 로컬 최적해를 찾는 문제로 접근해 문제를 더 작게 줄여나가는 형태로, 서로 반대 방향으로 접근하는 구조이다

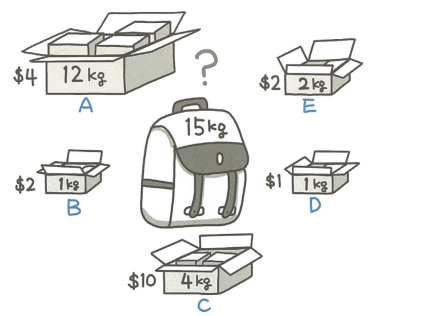
배낭 문제

• 배낭 문제는 조합 최적화에 대한 문제로 배낭에 담을 수 있는 무게의 최댓값이 정해져 있고 각각 짐의 가치와 무게가 있는 짐들을 배낭에 넣을 때 가치의 합이 최대로 되도록 선택하는 문제다

  

• 배낭 문제는 위 그림과 같은 분할 가능한 배낭 문제와 짐을 쪼갤 수 없는 경우인 0-1 배낭 문제(다이나믹 프로그래밍)로 나뉜다

def fractional_knapsack(cargo):
    capacity = 15
    pack = []
    # 단가 계산 역순 정렬
    for c in cargo:
        pack.append((c[0] / c[1], c[0], c[1]))
    pack.sort(reverse=True)

    # 단가 순 그리디 계산
    total_value: float = 0
    for p in pack:
        if capacity - p[2] >= 0:
            capacity -= p[2]
            total_value += p[1]
        else:
            fraction = capacity / p[2]
            total_value += p[1] * fraction
            break
    return total_value

• 단가가 가장 높은 짐부터 차례대로 채워가면 되는데 이 그림에는 C의 단가가 2.5달러로 가장 높다
• C, B, E, D 순으로 총 8kg의 짐을 배낭에 담고 마지막 남은 7kg을 위해 A의 $7 \over 12$만큼 쪼개서 배낭에 담는다
• fractional_knapsack 함수에서 먼저 단가를 계산하고 역순으로 정렬한다
• 가장 단가가 높은 짐이 맨 위에 오도록 한다
• 17.3이라는 최적해를 찾을 수 있다
• 하지만 짐을 쪼개지 못하는 문제에서는 이렇게 풀이할 수 없다

---

#78 주식을 사고팔기 가장 좋은 시점2

여러 번의 거래로 낼 수 있는 최대 이익을 산출하라

입력

[7, 1, 5, 3, 6, 4]

그리디 알고리즘

def best_sell_stock(day: list):
    result = 0
    # 값을 모르는 경우 매번 그리디 계산
    # 모두 비교해서 연산
    for i in range(len(day) - 1):
        if day[i + 1] > day[i]:
            result += day[i + 1] - day[i]

    return result

• 모든 경우를 비교한다
• 수수료를 신경쓰지 않아도 되고 값을 이미 알고 있으므로 그리디 연산이 가능하다

파이썬 다운 방식

def maxProfit(price: list) -> int:
    # 0보다 크면 무조건 합산
    return sum(max(price[i + 1] - price[i], 0) for i in range(len(price) - 1))

• 매번 이익을 계산헤서 0보다 크면 무조건 더하는 방식이다
• 그리디와 파이썬 다운 방식은 실행시간은 거의 비슷하다

---

#82 쿠키 부여

아이들에게 1개씩 쿠키를 나눠줘야 한다. 각 아이 child_i마다 그리드 팩터 $g_i$ 를 갖고 있으며, 이는 아이가 만족하는 최소 쿠키의 크기를 말한다. 각 쿠키 cookie_j는 크기 $s_j$ 를 갖고 있으며 $s_j >=g_i$ 이어야 아이가 만족하는 쿠키를 받는다. 최대 몇 명의 아이들에게 쿠키를 줄 수 있는지 출력하라

그리디 알고리즘

def findCounter(g: list, s: list) -> int:
    # EX: g: grid factor
    # EX: s: 쿠키 개수??
    g.sort()
    s.sort()

    child_i = cookies_j = 0
    # 만족하지 못 할때까지 그리디 진행
    while child_i < len(g) and cookies_j < len(s):
        if s[cookies_j] >= g[child_i]:
            child_i += 1
        cookies_j += 1

    return child_i

• 먼저 입력받은 리스트들을 정렬해야 한다
• 정렬 후 아이가 만족하는 개수가 존재할 경우 1씩 더해준다

이진 검색

def BST(g: list, s: list):
    g.sort()
    s.sort()

    result = 0
    for i in s:
        # 이진 검색으로 더 큰 인덱스 탐색
        index = bisect.bisect_right(g, i)
        if index > result:
            result += 1
    return result

• 하나의 리스트를 순회하면서 다른 하나는 이진 검색으로 찾는다
• 찾아낸 인덱스가 현재 부여한 아이들보다 클 경우에는 이 경우 더 줄 수 있으므로 1을 더해준다
• bisect_right는 찾아낸 값의 다음 인덱스를 리턴한고 bisect_left는 찾아낸 값의 해당 위치 인덱스를 리턴한다