다이나믹 프로그래밍 (Python Algorithm interview 23장)

파이썬 알고리즘 인터뷰 23장을 정리한 내용입니다.

다이나믹프로그래밍

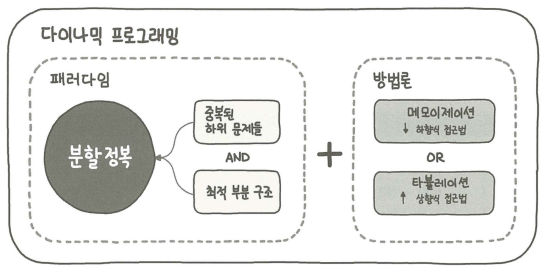
• 다이나믹프로그래밍 알고리즘은 문제를 각각의 작은 문제로 나누어 해결한 결과를 저장해뒀다가 나중에 큰 문제의 결과와 합하여 풀이하는 알고리즘이다
• 다이나믹 프로그래밍을 이용해 문제의 최적 해결 방법이 부분 문제에 대한 최적 해결 방법으로 구성되는 경우의 문제를 풀이할 수 있다
• 순간 최적을 선택하는 그리디 알고리즘과 많이 비교되며 다이타믹 프로그래밍은 중복된 하위 문제들의 결과를 저장했다가 풀이한다는 차이가 있다

최적 부분 구조

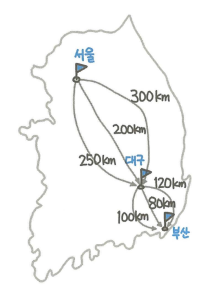
• 서울에서 부산까지 가는 최단 경로를 찾는 간단한 예이다
• 서울에서 대구까지는 3가지의 경로가 있고 부산까지도 3가지의 경로를 가지고 있다
• 서울에서 부산까지의 최단 경로는 $200km + 80km=280km$이다
• 위 경로는 서울에서 대구까지 가는 최단경로(200km)와 대구에서 부산까지 가는 최단 경로(80km)로 구성된다
• 서울에서 부산까지의 최단 경로는 (1)서울에서 대구까지 최단경로 (2)대구에서 부산까지 최단경로 두가지 부분 문제의 해답의 합이된다
• 이런 구조는 부분 문제에 대한 최적 해결 방법으로 구성되는 다이나믹 프로그래밍이다

다이나믹 프로그래밍 방법론

• 상향식과 하향식으로 나뉜다 상향식을 타블레이션, 하향식을 메모이제이션이라고도 한다

상향식

def fib(n):
    dp[0] = 0
    dp[1] = 1

    for i in range(2, n + 1):
        dp[i] = dp[i - 1] + dp[i - 2]
    return dp[n]

• 더 작은 하위 문제부터 살핀다음 작은 문제의 정답을 이용해 큰 문제의 정답을 풀어나간다
• 데이터를 테이블 형태로 만들면서 문제를 풀이한다

하향식

def fib_(n):
    if n <= 1:
        return n

    if dp[n]:
        return dp[n]
    dp[n] = fib(n - 1) + fib(n - 2)
    return dp[n]

• 하위 문제에 대한 정답을 계산했는지 확인해가며 문제를 자연스러운 방식으로 풀어나간다
• 재귀와 비슷하며 이미 풀어봤는지 확인하여 재활용하는 효율적인 방법이다

---

0-1 배낭 문제

쪼갤수 없는 배낭문제를 다이나믹 프로그래밍으로 푼다

• 모든 경우의 수를 계산해야 한다

def zero_one_knapsack(cargo):
    capacity = 15
    pack = []

    for i in range(len(cargo) + 1):
        pack.append([])
        for c in range(capacity + 1):
            if i == 0 or c == 0:
                pack[i].append(0)
            elif cargo[i - 1][1] <= c:
                pack[i].append(
                    max(
                        cargo[i - 1][0] + pack[i - 1][c - cargo[i - 1][1]],
                        pack[i - 1][c]
                    ))
            else:
                pack[i].append(pack[i - 1][c])

    return pack[-1][-1]

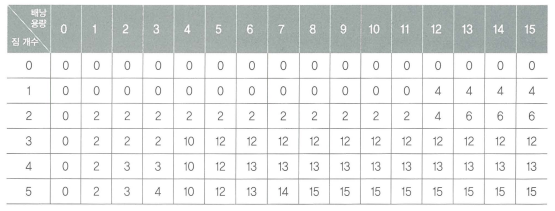
• pack에 중간 결과 테이블을 생성한다
• 테이블 크기의 기준은 짐의 최대 개수 +1, 배낭의 최대 용량 +1로 6X16이다
• 각 셀에는 위치까지의 짐의 개수와 배낭에 용량에 따른 최댓값이 담긴다
• 세로축은 짐의 개수, 가로축은 배낭의 용량이다
• 0-1 배낭문제를 타뷸레이션으로 풀었다

---

#86 최대 서브 배열

합이 최대가 되는 연속 서브 배열을 찾아 합을 리턴하라

다이나믹 프로그래밍(메모이제이션)

def maxSubArray(nums: list) -> int:
    for i in range(1, len(nums)):
        print(nums)
        nums[i] += nums[i - 1] if nums[i - 1] > 0 else 0
    return max(nums)

• 메모이제이션 풀이이다
• 앞에서부터 값을 계산하면서 누적 합을 계산한다
• 더해가면서 0이하일 경우에는 버린다
• 메모이제이션으로 더한 값들 중 최댓값을 반환하면 최대 합을 알 수 있다

카데인 알고리즘

def kadane(nums: list) -> int:
    best_sum = -sys.maxsize
    current_sum = 0
    for num in nums:
        print(f'num {num} current num {current_sum} best sum {best_sum}')
        current_sum = max(num, current_sum + num)
        best_sum = max(best_sum, current_sum)

    return best_sum

• 리스트의 숫자를 돌면서 매번 best_sum을 계산하여 반환한다
• 메모이제이션과 비슷하지만 개인적으로 카데인 알고리즘이 이해하기 편했다