이진 탐색 (이것이 취업을 위한 코딩 테스트다)

이것이 취업을 위한 코딩 테스트다를 정리한 글입니다.

순차 탐색

순차 탐색은 리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 차례대로 확인하는 방법이다. 리스트를 단순히 for문으로 돌면서 원하는 값을 찾는 경우도 순차 탐색이라고 볼 수 있다.

이진 탐색

이진 탐색은 배열 내부의 데이터가 정렬되어 있어야 사용할 수 있는 알고리즘이다. 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 이진 탐색은 시작점, 끝점, 중간점을 이용하여 탐색 범위를 설정한다.

찾으려는 데이터와 중간점위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾는 것이 이진 탐색이다.

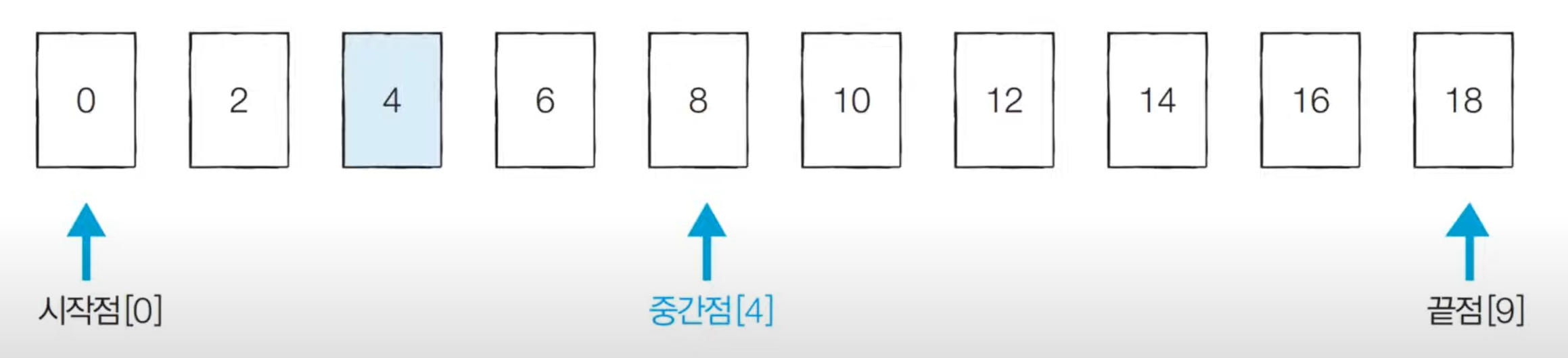
배열에서 4를 찾기 위한 이진 탐색의 동작을 알아보자.

1. 시작점, 중간점, 끝점을 이용해서 탐색을 시작한다.

찾으려는 값 4는 중간점의 값 8보다 작기 때문에 중간점 오른쪽에 있는 숫자들은 확인할 필요가 없어지고 왼쪽에 있는 값만 확인하면 된다.

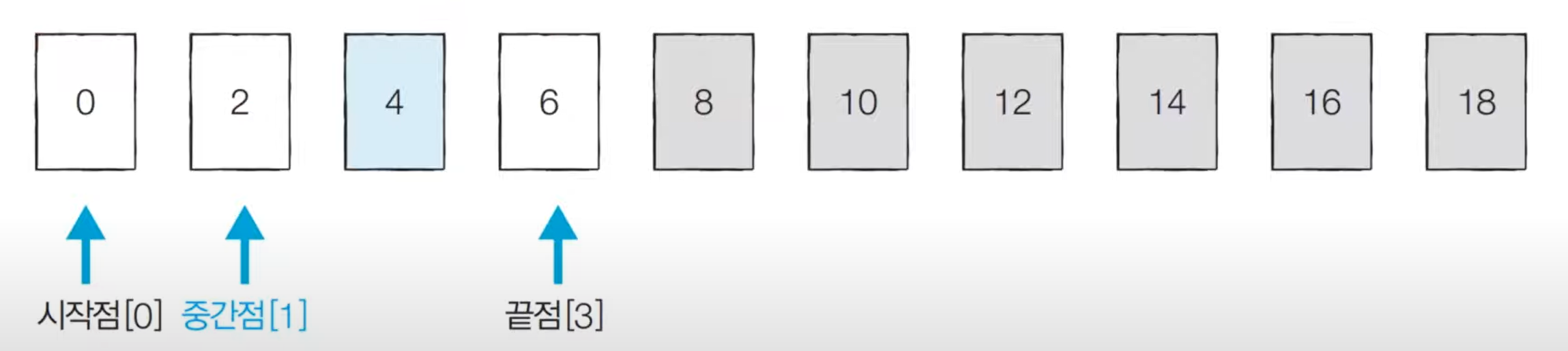
1. 1번에서의 중간점 왼쪽의 값들을 가지고 다시 시작점, 중간점, 끝점을 지정한다.

찾으려는 값 4는 중간점 값 2보다 크기 때문에 이제 중간점 오른쪽에 있는 값들만 확인하면 된다.

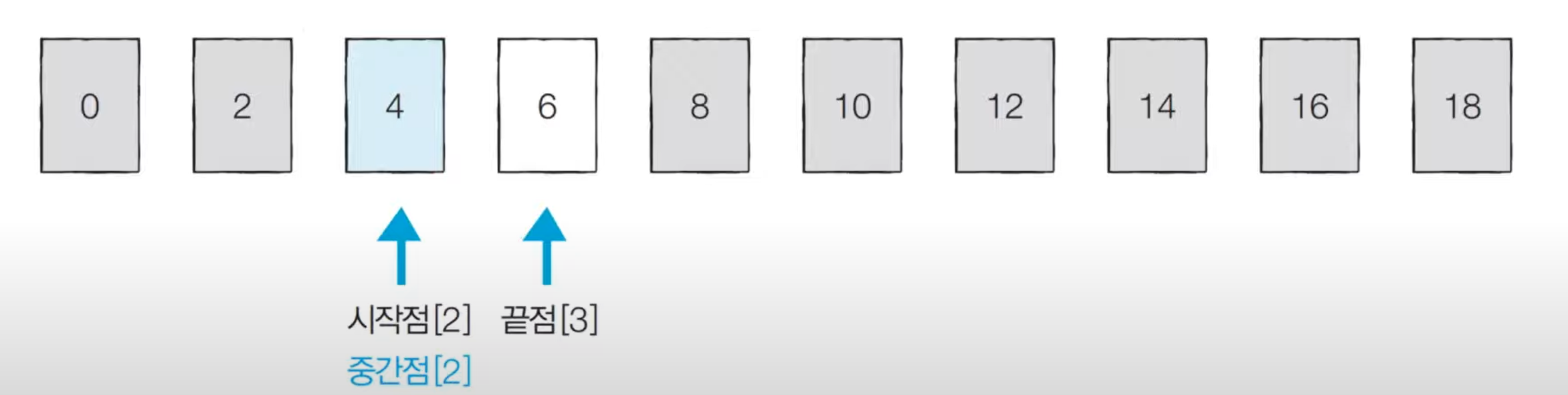
1. 2번에서의 중간점 오른쪽의 값들을 가지고 확인을 해보면 시작점과 중간점이 4로 동일하게 되며 찾으려는 값이다.

이진 탐색의 시간 복잡도

이진 탐색의 시간 복잡도는 단계마다 탐색 범위를 2로 나누는 것과 동일하므로 연산 횟수는 $\log_2N$에 비례한다. 예를 들어 데이터 개수가 32개일 경우 1단꼐를 거치면 16개의 데이터가 남게 된다. 이진 탐색의 시간 복잡도를 빅-오 표기법으로 나타내면 $O(\log_2N)$으로 나타낼 수 있다.

이진 탐색의 재귀적 구현

# 이진 탐색 소스코드 구현 (재귀 함수)
def binary_search(array, target, start, end):
    if start > end:
        return None
    mid = (start + end) // 2
    # 찾은 경우 중간점 인덱스 반환
    if array[mid] == target:
        return mid
    # 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
    elif array[mid] > target:
        return binary_search(array, target, start, mid - 1)
    # 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
    else:
        return binary_search(array, target, mid + 1, end)

# n(원소의 개수)과 target(찾고자 하는 값)을 입력 받기
n, target = list(map(int, input().split()))
# 전체 원소 입력 받기
array = list(map(int, input().split()))

# 이진 탐색 수행 결과 출력
result = binary_search(array, target, 0, n - 1)
if result == None:
    print("원소가 존재하지 않습니다.")
else:
    print(result + 1)

몫을 구하는 //연산자로 mid값을 지정해 탐색을 이어나간다. 찾고자 하는 값이 중간값보다 크면 start는 start, end는 mid - 1로 입력이 들어가고, 작으면 start는 mid + 1, end는 end로 입력을 사용해 재귀적으로 구현한다.

트리 자료구조

이진 탐색을 사용할 수 있는 조건은 정렬된 데이터인 경우다. 트리 자료구조는 노드와 노드의 연결로 표현되며 루트 노드, 서브 트리, 단말 노드로 구성되어 있다. 트리의 특징은 다음과 같다.

• 트리의 부모 노드와 자식 노드의 관계로 표현된다.
• 트리의 최상단 노드를 루트 노드라고 한다.
• 트리의 최하단 노드를 단말 노드라고 한다.
• 트리에서 일부를 떼어내도 트리 구조이며 이를 서브 트리라고 한다.
• 트리는 파일 시스템과 같이 계층적이고 정렬된 데이터를 다루기에 적합하다.

이진 탐색 트리

이진 탐색이 동작할 수 있도록 효율적으로 구현된 트리 구조는 이진 탐색 트리이다. 이진 탐색 트리의 특징은 다음과 같다.

• 부모 노드보다 왼쪽 자식 노드가 작다.
• 부모 노드보다 오른쪽 자식 노드가 크다.

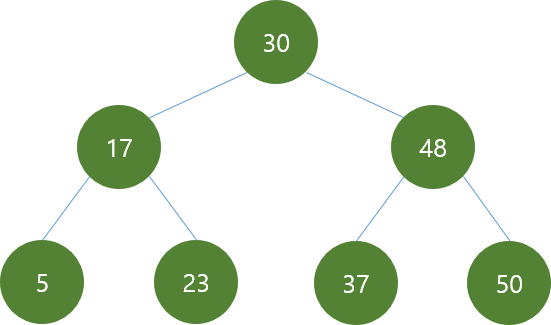
이진 탐색 트리에서 값 조회하기

위 이진 탐색 트리에서 37을 조회하는 과정을 간단하게 살펴 본다.

1. 루트 노드인 30을 시작으로 탐색한다. 37은 루트 노드보다 큰 값이므로 37은 오른쪽 서브 트리에 존재할 것이다. 30의 오른쪽 서브트리를 탐색한다.
2. 48이 부모 노드가 된다. 찾고자 하는 값 37보다 부모 노드가 크기 때문에 왼쪽 서브 트리를 탐색하면 될 것이다.
3. 왼쪽 노드를 탐색 하게 되면 target 값인 37을 찾을 수 있다.

빠르게 입력 받기

데이터의 개수가 1,000만개가 넘어가거나 탐색 범위의 크기가 1,000억 이상인 경우 이진 탐색을 사용해야 할 가능성이 클 것이다. 이런 경우 입력 데이터의 개수가 많은 문제에 input()함수를 사용하면 동작 속도가 느려서 시간 초과가 발생할 수 있다. sys라이브러리의 readline()함수를 사용하면 시간 초과를 피할 수 있다.

import sys

# 하나의 문자열 데이터 입력 받기
input_data = sys.stdin.readline().rstrip()
# 입력 받은 문자열 그대로 출력하기
print(input_data)

sys라이브러리를 사용한 입력은 한 줄씩 받게 된다.